Model Diagnostics and Exam 1 Review

STA 210 - Summer 2022

Author

Yunran Chen

Announcements

  • Exam 1 opens today at 1:00 pm and ends on Monday, May 23 at 11:59pm.

Feedback from submissions so far

  • You must submit a PDF (not HTML) to Gradescope
  • You must tag your pages when you upload to Gradescope – if you don’t know how to do this, please ask well before the deadline!
  • You must not refer to keys distributed in previous semesters of the course – much of what we’re doing is different and some of it is the same. If you need help, please ask!

Exam 1

  • Instructions can be found at website
  • Covers everything we’ve done so far
  • Any clarification questions for the exam?
    • Post on Sakai Conversations, post to “Instructors in this site”

Interpretation on CI

We are 95% confident that, as xx increase by 1 unit, the model predicts xx increase/decrease [,] on average.

We are 95% confident that mean sale price of Duke Forest houses that are 2,800 square feet is between XX and XX.

Tips on R programming

library(tidyverse)
test <- tibble(a=1,b=2)
test
# A tibble: 1 × 2
      a     b
  <dbl> <dbl>
1     1     2

The test values are 1 and 2.

Outliers and influential points

Outliers

  • Boxplot
  • Standard residuals

Identifying influential points

  • Leverage
  • Standardized residuals
  • Cook’s Distance
library(tidyverse)
library(knitr)
library(broom)
library(patchwork)
library(kableExtra)
library(ggfortify)
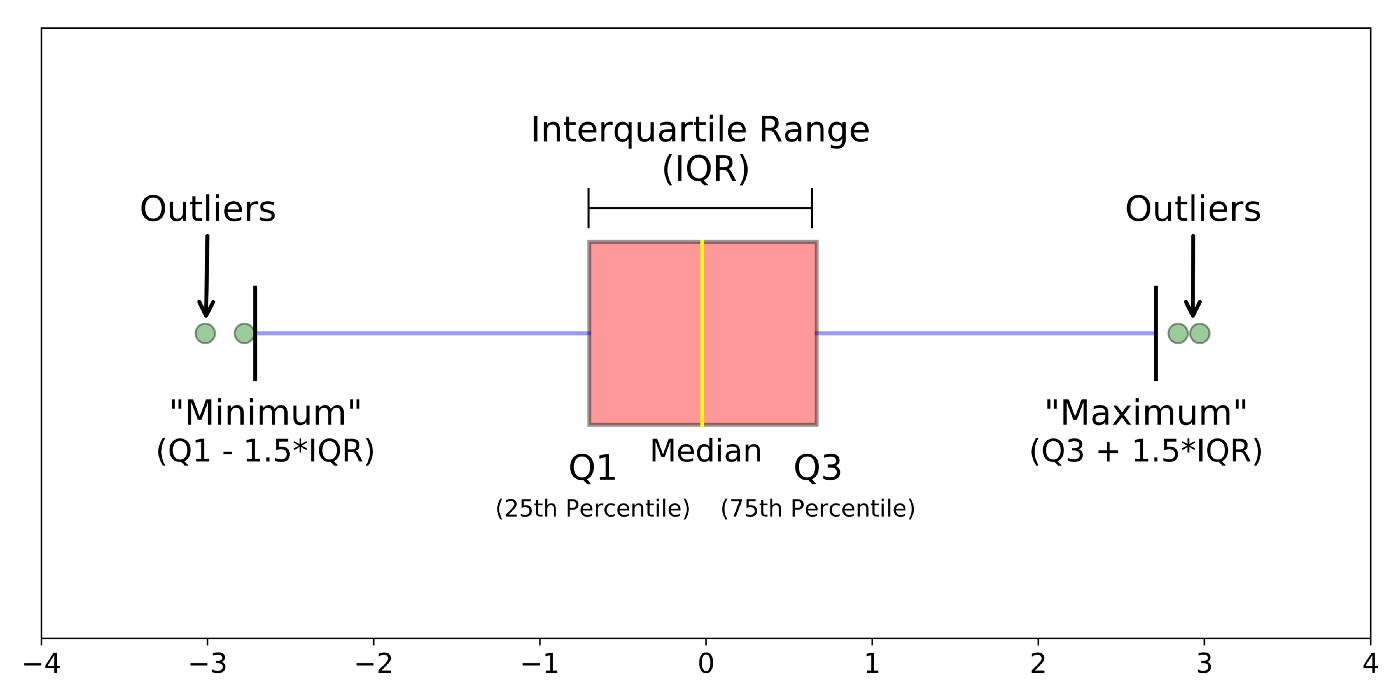
library(viridis)

Influential Point

An observation is influential if removing it substantially changes the coefficients of the regression model

Influential points

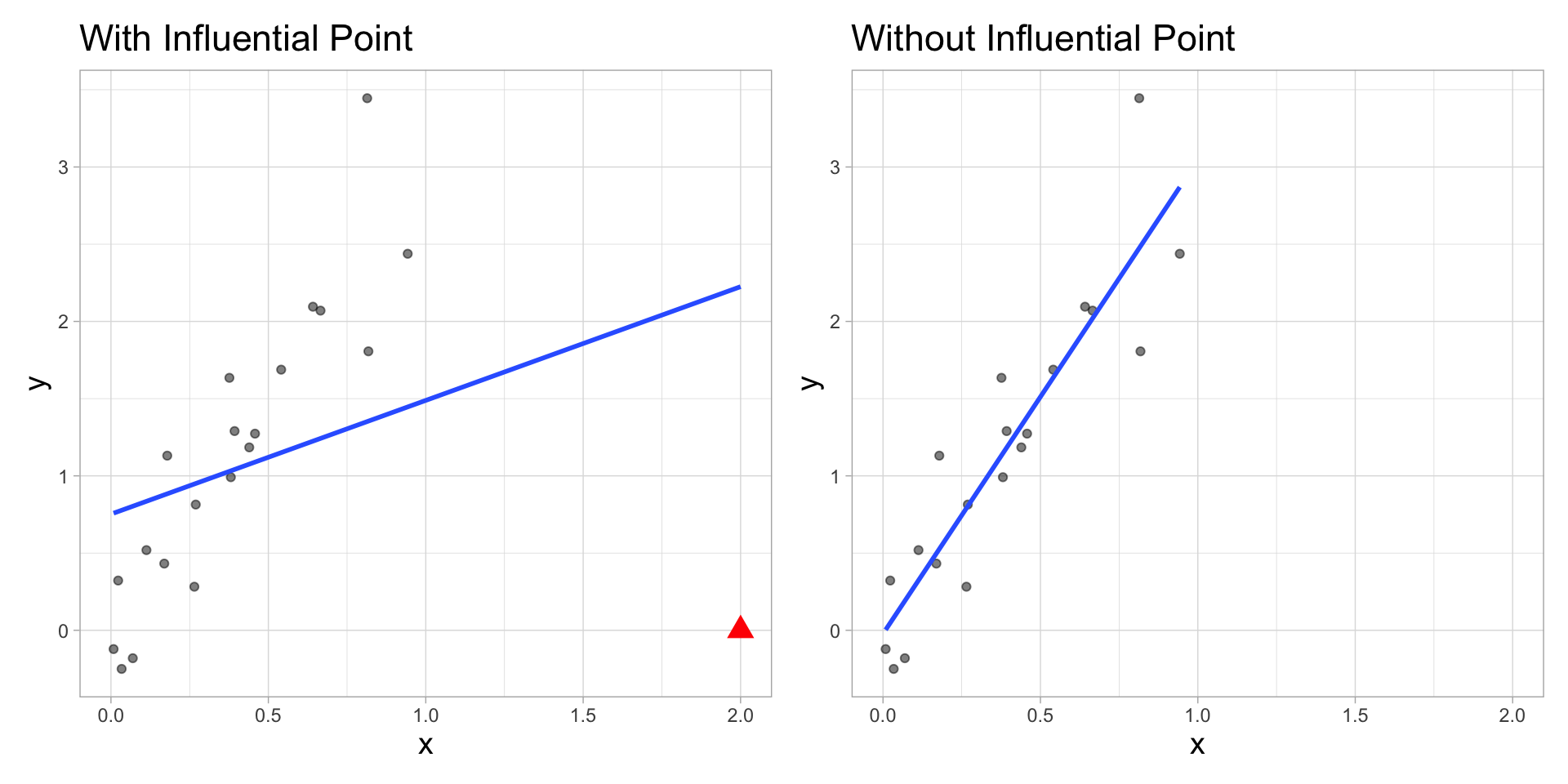
  • Influential points have a large impact on the coefficients and standard errors used for inference

  • These points can sometimes be identified in a scatterplot if there is only one predictor variable

    • This is often not the case when there are multiple predictors

  • We will use measures to quantify an individual observation’s influence on the regression model

    • leverage, standardized residuals, and Cook’s distance

Model diagnostics in R

Use the augment function to output the model diagnostics (along with the predicted values and residuals)

  • response and predictor variables in the model
  • .fitted: predicted values
  • .se.fit: standard errors of predicted values
  • .resid: residuals
  • .hat: leverage
  • .sigma: estimate of residual standard deviation when the corresponding observation is dropped from model
  • .cooksd: Cook’s distance
  • .std.resid: standardized residuals

Example: Average SAT scores by state

  • This data set contains the average SAT score (out of 1600) and other variables that may be associated with SAT performance for each of the 50 U.S. states. The data is based on test takers for the 1982 exam.

  • Response - .vocab[SAT]: average total SAT score

  • Predictor - .vocab[Public]: percentage of test-takers who attended public high schools

.footnote[Data comes from case1201 data set in the Sleuth3 package]

Model

sat_scores <- Sleuth3::case1201
sat_model <- lm(SAT ~ Public, data = sat_scores)
tidy(sat_model) %>%
  kable(digits = 3)
term estimate std.error statistic p.value
(Intercept) 994.971 84.807 11.732 0.000
Public -0.579 1.037 -0.559 0.579

SAT: Augmented Data

sat_aug = augment(sat_model) %>%
  mutate(obs_num=row_number())
glimpse(sat_aug)
Rows: 50
Columns: 9
$ SAT        <int> 1088, 1075, 1068, 1045, 1045, 1033, 1028, 1022, 1017, 1011,…
$ Public     <dbl> 87.8, 86.2, 88.3, 83.9, 83.6, 93.7, 78.3, 75.2, 97.0, 77.3,…
$ .fitted    <dbl> 944.1198, 945.0465, 943.8302, 946.3786, 946.5523, 940.7027,…
$ .resid     <dbl> 143.880224, 129.953547, 124.169810, 98.621450, 98.447698, 9…
$ .hat       <dbl> 0.02918707, 0.02527061, 0.03063269, 0.02153481, 0.02121224,…
$ .sigma     <dbl> 68.89683, 69.51144, 69.72849, 70.63271, 70.63847, 70.77489,…
$ .cooksd    <dbl> 0.0629494764, 0.0441056591, 0.0493526954, 0.0214814500, 0.0…
$ .std.resid <dbl> 2.0463672, 1.8445751, 1.7673480, 1.3971689, 1.3944776, 1.32…
$ obs_num    <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, …

Leverage

  • Leverage: measure of the distance between an observation’s values of the predictor variables and the average values of the predictor variables for the entire data set

  • An observation has high leverage if its combination of values for the predictor variables is very far from the typical combination of values in the data

  • Observations with high leverage should be considered as potential influential points

Calculating leverage

Simple Regression: leverage of the \(i^{th}\) observation \[h_i = \frac{1}{n} + \frac{(x_i - \bar{x})^2}{\sum_{j=1}^{n}(x_j-\bar{x})^2}\]

  • Note: Leverage only depends on values of the predictor variable(s)

High Leverage

  • The sum of the leverages for all points is \(p + 1\)

  • \(p\) is the number of predictors

  • In the case of SLR \(\sum_{i=1}^n h_i = 2\)

  • The “typical” leverage is \(\frac{(p+1)}{n}\)

  • An observation has high leverage if \[h_i > \frac{2(p+1)}{n}\]

High Leverage

If there is point with high leverage, ask

  • Is there a data entry error?

  • Is this observation within the scope of individuals for which you want to make predictions and draw conclusions?

  • Is this observation impacting the estimates of the model coefficients, especially for interactions?

Just because a point has high leverage does not necessarily mean it will have a substantial impact on the regression. Therefore we need to check other measures.

SAT: Leverage

Observations with high leverage

(leverage_threshold <- 2*(1+1)/nrow(sat_aug))
[1] 0.08
autoplot(sat_model,which = 5, ncol = 1) + 
  geom_vline(xintercept = leverage_threshold, color = "red")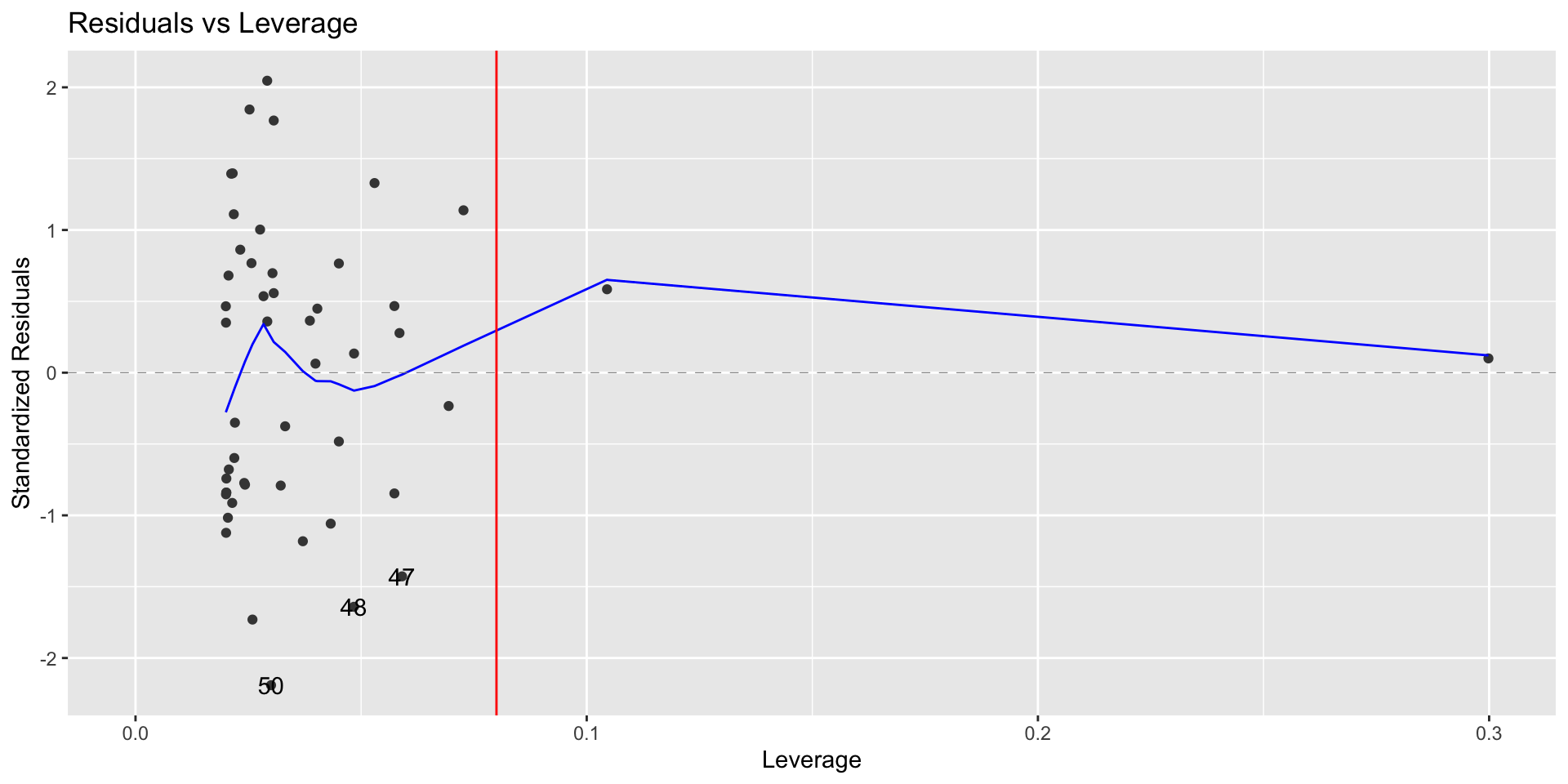

sat_aug %>% filter(.hat > leverage_threshold) %>% 
  select(SAT, Public)
# A tibble: 2 × 2
    SAT Public
  <int>  <dbl>
1   999   61.2
2   975   44.8

Why do you think these observations have high leverage?

Let’s dig into the data

Standardized residuals

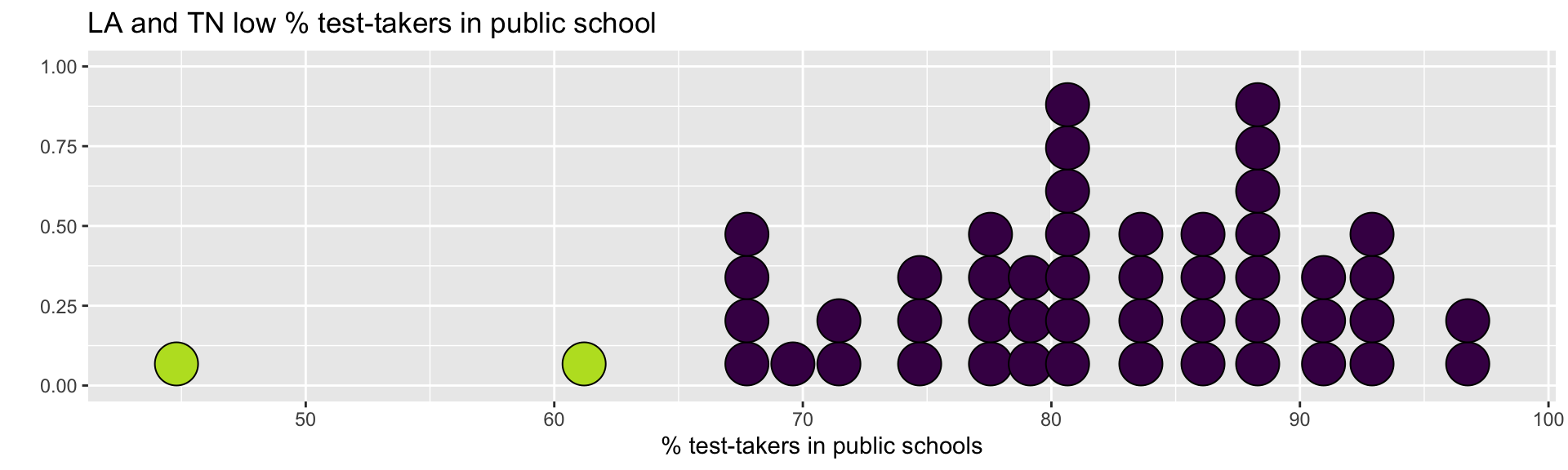
  • What is the best way to identify outliers (points that don’t fit the pattern from the regression line)?

  • Look for points that have large residuals

  • We want a common scale, so we can more easily identify “large” residuals

  • We will look at each residual divided by its standard error

Standardized residuals

\[std.res_i = \frac{y_i - \hat{y}_i}{\hat{\sigma}_\epsilon\sqrt{1-h_i}}\]

  • Standardized residuals are produced by augment in the column .std.resid

Standardized residuals

Observations with high leverage tend to have low values of standardized residuals because they pull the regression line towards them

autoplot(sat_model, which = 5, ncol = 1)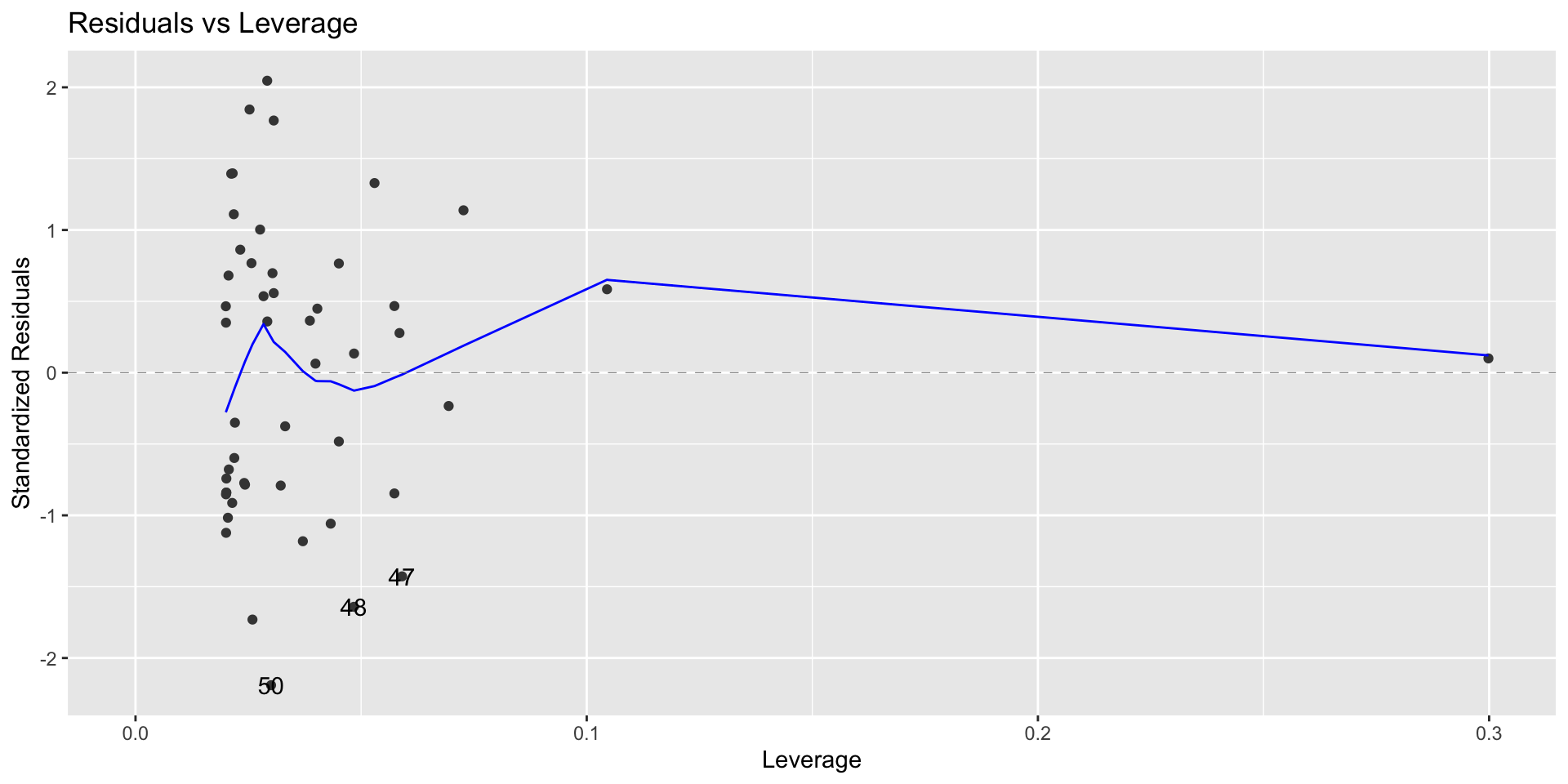

Using standardized residuals

Observations that have standardized residuals of large magnitude are outliers, since they don’t fit the pattern determined by the regression model

An observation is a potential outlier if its standardized residual is beyond \(\pm 3\).

Make residual plots with standardized residuals to make it easier to identify outliers

autoplot(sat_model, which = 3, ncol = 1) + 
  geom_hline(yintercept = sqrt(3),color = "red",linetype = "dotted")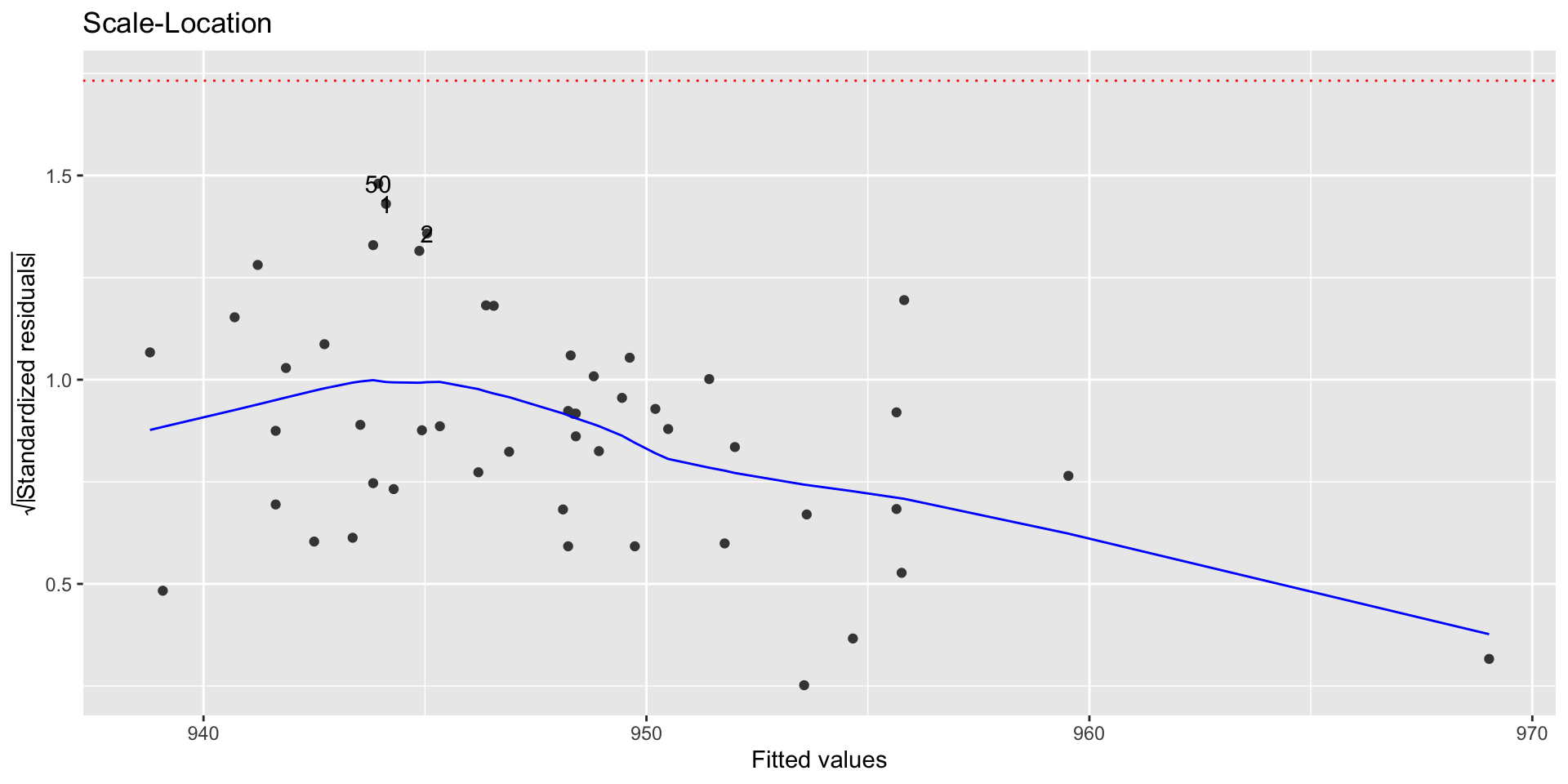

Motivating Cook’s Distance

An observation’s influence on the regression line depends on

  • How close it lies to the general trend of the data - (Standardized residual)

  • Its leverage - \(h_i\)

Cook’s Distance is a statistic that includes both of these components to measure an observation’s overall impact on the model

Cook’s Distance

Cook’s distance for the \(i^{th}\) observation

An observation with large \(D_i\) is said to have a strong influence on the predicted values

An observation with

  • \(D_i > 0.5\) is moderately influential
  • \(D_i > 1\) is very influential

Cook’s Distance

autoplot(sat_model, which = 4, ncol = 1) + 
  geom_hline(yintercept = 0.5, color = "red", lty = 2) +
  geom_hline(yintercept = 1,color = "red")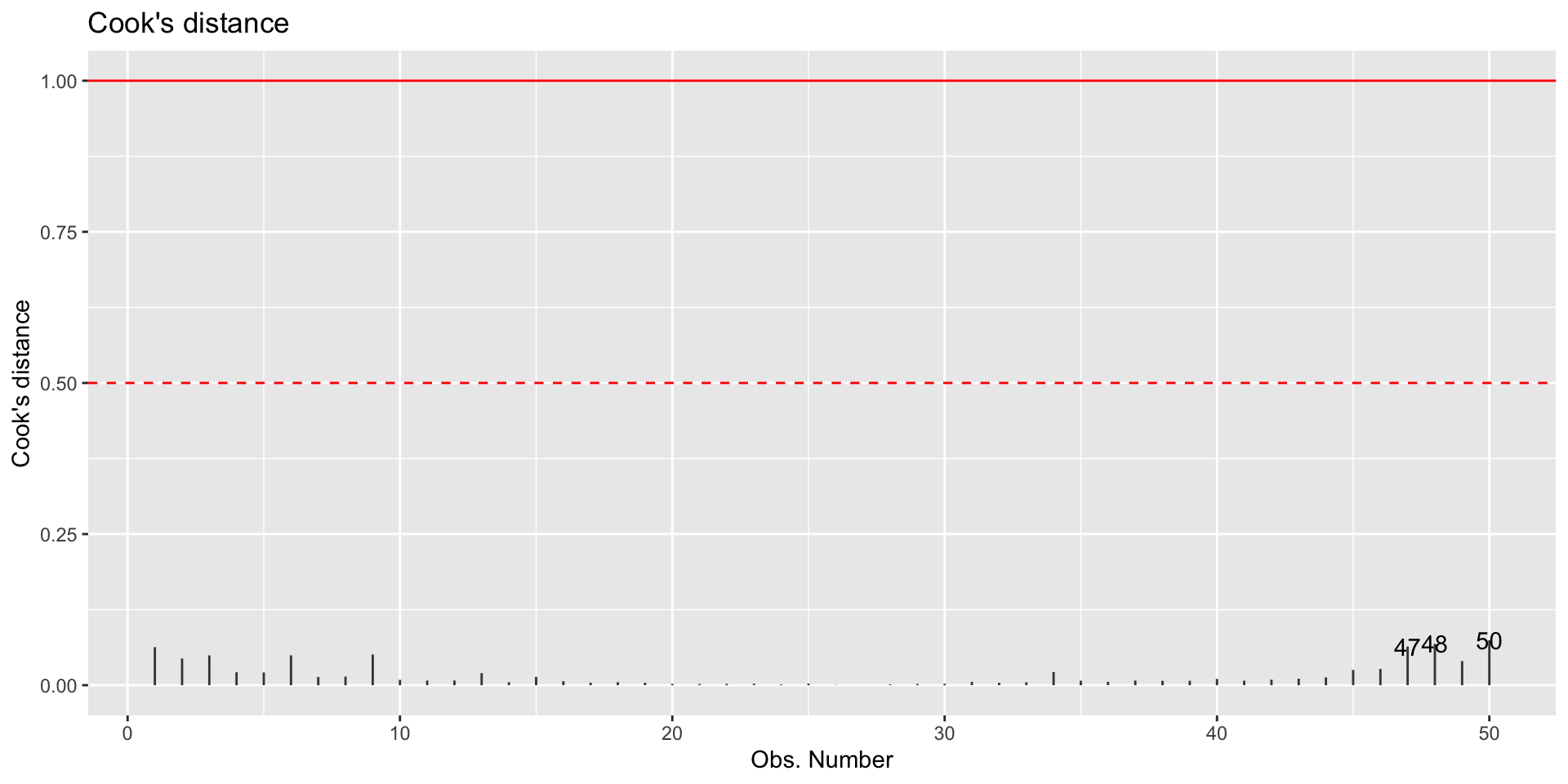

Using these measures

  • Standardized residuals, leverage, and Cook’s Distance should all be examined together

  • Examine plots of the measures to identify observations that are outliers, high leverage, and may potentially impact the model.

What to do with outliers/influential points?

It is OK to drop an observation based on the predictor variables if…

  • It is meaningful to drop the observation given the context of the problem

  • You intended to build a model on a smaller range of the predictor variables. Mention this in the write up of the results and be careful to avoid extrapolation when making predictions

What to do with outliers/influential points?

It is not OK to drop an observation based on the response variable

  • These are legitimate observations and should be in the model

  • You can try transformations or increasing the sample size by collecting more data

–

In either instance, you can try building the model with and without the outliers/influential observations

Application Exercise

📋 github.com/STA210-Summer22/ae-4