LR: Inference + comparison + conditions

STA 210 - Summer 2022

Author

Yunran Chen

Welcome

Computational setup

# load packages
library(tidyverse)
library(tidymodels)
library(openintro)
library(knitr)
library(kableExtra)  # for table embellishments
library(Stat2Data)   # for empirical logit

# set default theme and larger font size for ggplot2
ggplot2::theme_set(ggplot2::theme_minimal(base_size = 20))

Data

Risk of coronary heart disease

This dataset is from an ongoing cardiovascular study on residents of the town of Framingham, Massachusetts. We want to examine the relationship between various health characteristics and the risk of having heart disease.

  • high_risk:

    • 1: High risk of having heart disease in next 10 years
    • 0: Not high risk of having heart disease in next 10 years

  • age: Age at exam time (in years)

  • education: 1 = Some High School, 2 = High School or GED, 3 = Some College or Vocational School, 4 = College

  • currentSmoker: 0 = nonsmoker, 1 = smoker

Data prep

heart_disease <- read_csv(here::here("slides", "data/framingham.csv")) %>%
  select(age, education, TenYearCHD, totChol, currentSmoker) %>%
  drop_na() %>%
  mutate(
    high_risk = as.factor(TenYearCHD),
    education = as.factor(education),
    currentSmoker = as.factor(currentSmoker)
  )

heart_disease
# A tibble: 4,086 × 6
     age education TenYearCHD totChol currentSmoker high_risk
   <dbl> <fct>          <dbl>   <dbl> <fct>         <fct>    
 1    39 4                  0     195 0             0        
 2    46 2                  0     250 0             0        
 3    48 1                  0     245 1             0        
 4    61 3                  1     225 1             1        
 5    46 3                  0     285 1             0        
 6    43 2                  0     228 0             0        
 7    63 1                  1     205 0             1        
 8    45 2                  0     313 1             0        
 9    52 1                  0     260 0             0        
10    43 1                  0     225 1             0        
# … with 4,076 more rows

Inference for a model

Modeling risk of coronary heart disease

From age and education:

risk_fit <- logistic_reg() %>%
  set_engine("glm") %>%
  fit(high_risk ~ age + education, 
      data = heart_disease, family = "binomial")

Model output

tidy(risk_fit, conf.int = TRUE) %>% 
  kable(format = "markdown", digits = 3)
term estimate std.error statistic p.value conf.low conf.high
(Intercept) -5.508 0.311 -17.692 0.000 -6.125 -4.904
age 0.076 0.006 13.648 0.000 0.065 0.087
education2 -0.245 0.113 -2.172 0.030 -0.469 -0.026
education3 -0.236 0.135 -1.753 0.080 -0.504 0.024
education4 -0.024 0.150 -0.161 0.872 -0.323 0.264

\[ \small{\log\Big(\frac{\hat{\pi}}{1-\hat{\pi}}\Big) = -5.508 + 0.076 ~ \text{age} - 0.245 ~ \text{ed2} - 0.236 ~ \text{ed3} - 0.024 ~ \text{ed4}} \]

Cold Call

Confidence interval for \(\beta_j\)

We can calculate the \(C\%\) confidence interval for \(\beta_j\) as the following:

\[ \Large{\hat{\beta}_j \pm z^* SE_{\hat{\beta}_j}} \]

where \(z^*\) is calculated from the \(N(0,1)\) distribution

This is an interval for the change in the log-odds for every one unit increase in \(x_j\).

Interpretation in terms of the odds

The change in odds for every one unit increase in \(x_j\).

\[ \Large{e^{\hat{\beta}_j \pm z^* SE_{\hat{\beta}_j}}} \]

Interpretation: We are \(C\%\) confident that for every one unit increase in \(x_j\), the model predicts the odds multiply by a factor of \(e^{\hat{\beta}_j - z^* SE_{\hat{\beta}_j}}\) to \(e^{\hat{\beta}_j + z^* SE_{\hat{\beta}_j}}\), holding all else constant.

Coefficient for age

term estimate std.error statistic p.value conf.low conf.high
(Intercept) -5.508 0.311 -17.692 0.000 -6.125 -4.904
age 0.076 0.006 13.648 0.000 0.065 0.087
education2 -0.245 0.113 -2.172 0.030 -0.469 -0.026
education3 -0.236 0.135 -1.753 0.080 -0.504 0.024
education4 -0.024 0.150 -0.161 0.872 -0.323 0.264

Hypothesis test for \(\beta_j\)

Hypotheses: \(H_0: \beta_j = 0 \hspace{2mm} \text{ vs } \hspace{2mm} H_a: \beta_j \neq 0\)

Test Statistic: \[z = \frac{\hat{\beta}_j - 0}{SE_{\hat{\beta}_j}}\]

P-value: \(P(|Z| > |z|)\), where \(Z \sim N(0, 1)\), the Standard Normal distribution

Coefficient for age

term estimate std.error statistic p.value conf.low conf.high
(Intercept) -5.508 0.311 -17.692 0.000 -6.125 -4.904
age 0.076 0.006 13.648 0.000 0.065 0.087
education2 -0.245 0.113 -2.172 0.030 -0.469 -0.026
education3 -0.236 0.135 -1.753 0.080 -0.504 0.024
education4 -0.024 0.150 -0.161 0.872 -0.323 0.264

Hypotheses:

\[ H_0: \beta_{1} = 0 \hspace{2mm} \text{ vs } \hspace{2mm} H_a: \beta_{1} \neq 0 \]

Test statistic:

\[ z = \frac{0.07558692 - 0}{0.005538154} = 13.6484 \]

Coefficient for age

term estimate std.error statistic p.value conf.low conf.high
(Intercept) -5.508 0.311 -17.692 0.000 -6.125 -4.904
age 0.076 0.006 13.648 0.000 0.065 0.087
education2 -0.245 0.113 -2.172 0.030 -0.469 -0.026
education3 -0.236 0.135 -1.753 0.080 -0.504 0.024
education4 -0.024 0.150 -0.161 0.872 -0.323 0.264

P-value:

\[ P(|Z| > |13.648|) \approx 0 \]

2 * pnorm(13.648,lower.tail = FALSE)
[1] 2.074954e-42

Coefficient for age

term estimate std.error statistic p.value conf.low conf.high
(Intercept) -5.508 0.311 -17.692 0.000 -6.125 -4.904
age 0.076 0.006 13.648 0.000 0.065 0.087
education2 -0.245 0.113 -2.172 0.030 -0.469 -0.026
education3 -0.236 0.135 -1.753 0.080 -0.504 0.024
education4 -0.024 0.150 -0.161 0.872 -0.323 0.264

Conclusion:

The p-value is very small, so we reject \(H_0\). The data provide sufficient evidence that age is a statistically significant predictor of whether someone is high risk of having heart disease, after accounting for education.

Comparing models

Log likelihood

\[ \log L = \sum\limits_{i=1}^n[y_i \log(\hat{\pi}_i) + (1 - y_i)\log(1 - \hat{\pi}_i)] \]

  • Measure of how well the model fits the data

  • Higher values of \(\log L\) are better

  • Deviance = \(-2 \log L\)

    • \(-2 \log L\) follows a \(\chi^2\) distribution with \(n - p - 1\) degrees of freedom

Comparing nested models

  • Suppose there are two models:

    • Reduced Model includes predictors \(x_1, \ldots, x_q\)
    • Full Model includes predictors \(x_1, \ldots, x_q, x_{q+1}, \ldots, x_p\)

  • We want to test the hypotheses

    \[ \begin{aligned} H_0&: \beta_{q+1} = \dots = \beta_p = 0 \\ H_A&: \text{ at least 1 }\beta_j \text{ is not } 0 \end{aligned} \]

  • To do so, we will use the Drop-in-deviance test, also known as the Nested Likelihood Ratio test

Drop-in-deviance test

Hypotheses:

\[ \begin{aligned} H_0&: \beta_{q+1} = \dots = \beta_p = 0 \\ H_A&: \text{ at least 1 }\beta_j \text{ is not } 0 \end{aligned} \]

Test Statistic: \[G = (-2 \log L_{reduced}) - (-2 \log L_{full})\]

P-value: \(P(\chi^2 > G)\), calculated using a \(\chi^2\) distribution with degrees of freedom equal to the difference in the number of parameters in the full and reduced models

\(\chi^2\) distribution

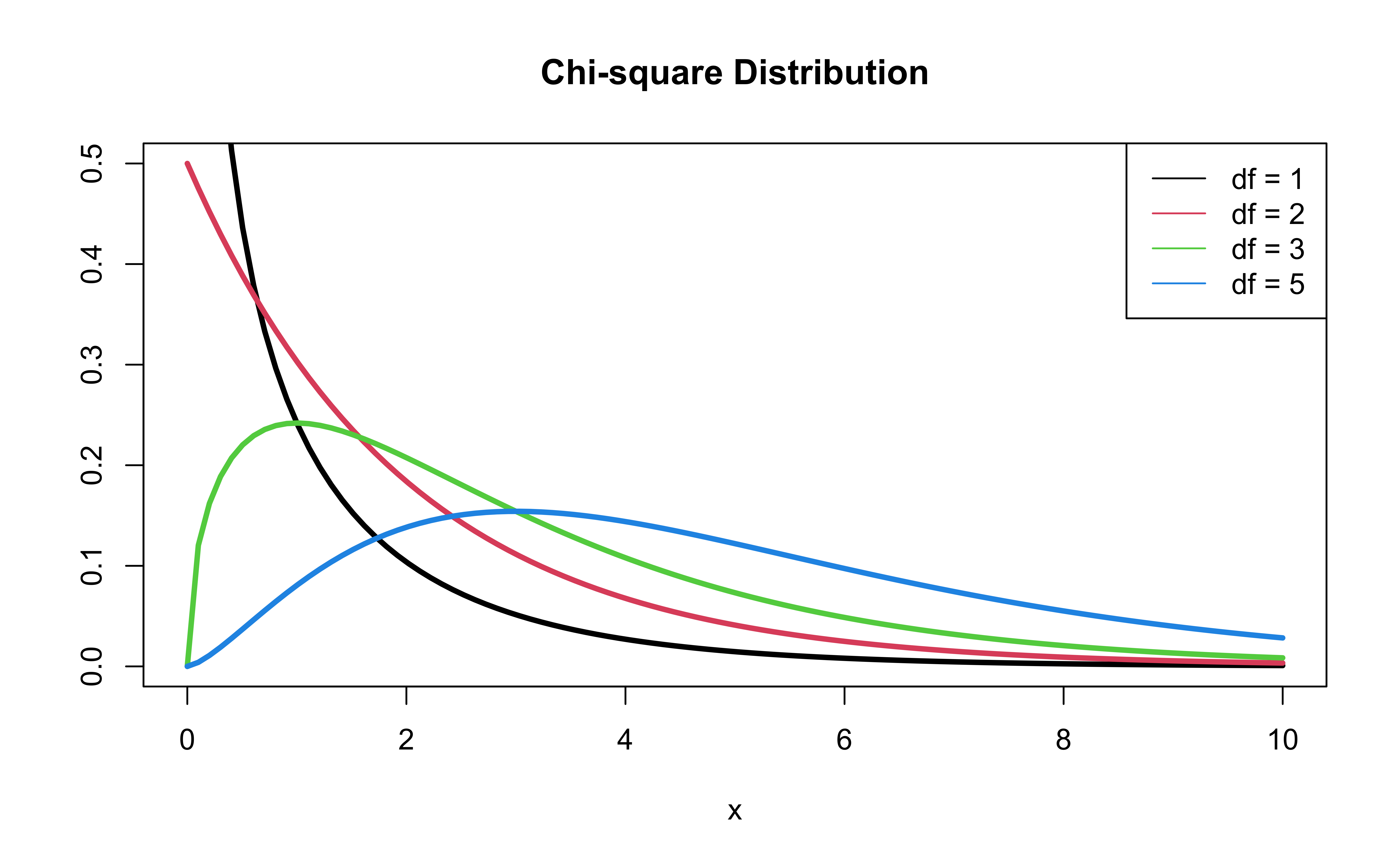
Model with age and education

Should we add currentSmoker to this model?

term estimate std.error statistic p.value conf.low conf.high
(Intercept) -5.508 0.311 -17.692 0.000 -6.125 -4.904
age 0.076 0.006 13.648 0.000 0.065 0.087
education2 -0.245 0.113 -2.172 0.030 -0.469 -0.026
education3 -0.236 0.135 -1.753 0.080 -0.504 0.024
education4 -0.024 0.150 -0.161 0.872 -0.323 0.264

Should we add currentSmoker to the model?

First model, reduced:

risk_fit_reduced <- logistic_reg() %>%
  set_engine("glm") %>%
  fit(high_risk ~ age + education, 
      data = heart_disease, family = "binomial")


Second model, full:

risk_fit_full <- logistic_reg() %>%
  set_engine("glm") %>%
  fit(high_risk ~ age + education + currentSmoker, 
      data = heart_disease, family = "binomial")

Should we add currentSmoker to the model?

Calculate deviance for each model:

(dev_reduced <- glance(risk_fit_reduced)$deviance)
[1] 3244.187
(dev_full <- glance(risk_fit_full)$deviance)
[1] 3221.901

Drop-in-deviance test statistic:

(test_stat <- dev_reduced - dev_full)
[1] 22.2863

Should we add currentSmoker to the model?

Calculate the p-value using a pchisq(), with degrees of freedom equal to the number of new model terms in the second model:

pchisq(test_stat, 1, lower.tail = FALSE) 
[1] 2.348761e-06

Conclusion: The p-value is very small, so we reject \(H_0\). The data provide sufficient evidence that the coefficient of currentSmoker is not equal to 0. Therefore, we should add it to the model.

Drop-in-Deviance test in R

  • We can use the anova function to conduct this test

  • Add test = "Chisq" to conduct the drop-in-deviance test

  • For linear regression nested models, we use F-stat to test . . .

anova(risk_fit_reduced$fit, risk_fit_full$fit, test = "Chisq") %>%
  tidy()
# A tibble: 2 × 5
  Resid..Df Resid..Dev    df Deviance     p.value
      <dbl>      <dbl> <dbl>    <dbl>       <dbl>
1      4081      3244.    NA     NA   NA         
2      4080      3222.     1     22.3  0.00000235

Model selection

Use AIC or BIC for model selection

\[ \begin{align} &AIC = - 2 * \log L - \color{purple}{n\log(n)}+ 2(p +1)\\[5pt] &BIC =- 2 * \log L - \color{purple}{n\log(n)} + log(n)\times(p+1) \end{align} \]

AIC from the glance() function

Let’s look at the AIC for the model that includes age, education, and currentSmoker

glance(risk_fit_full)$AIC
[1] 3233.901

Calculating AIC

- 2 * glance(risk_fit_full)$logLik + 2 * (5 + 1)
[1] 3233.901

Comparing the models using AIC

Let’s compare the full and reduced models using AIC.

glance(risk_fit_reduced)$AIC
[1] 3254.187
glance(risk_fit_full)$AIC
[1] 3233.901

Based on AIC, which model would you choose?

Comparing the models using BIC

Let’s compare the full and reduced models using BIC

glance(risk_fit_reduced)$BIC
[1] 3285.764
glance(risk_fit_full)$BIC
[1] 3271.793

Based on BIC, which model would you choose?

Comparing the models using ROC-AUC

risk_pred_reduced <- predict(risk_fit_reduced, heart_disease, type = "prob") %>% 
  bind_cols(heart_disease) 
risk_pred_reduced %>%
  roc_auc(
    truth = high_risk,
    .pred_1,
    event_level = "second"
  )
# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 roc_auc binary         0.688
risk_pred_full <- predict(risk_fit_full, heart_disease, type = "prob") %>% 
  bind_cols(heart_disease) 
risk_pred_full %>%
  roc_auc(
    truth = high_risk,
    .pred_1,
    event_level = "second"
  )
# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 roc_auc binary         0.696

Conditions

The model

Let’s predict high_risk from age, total cholesterol, and whether the patient is a current smoker:

risk_fit <- logistic_reg() %>%
  set_engine("glm") %>%
  fit(high_risk ~ age + totChol + currentSmoker, 
      data = heart_disease, family = "binomial")

tidy(risk_fit, conf.int = TRUE) %>% 
  kable(digits = 3)
term estimate std.error statistic p.value conf.low conf.high
(Intercept) -6.673 0.378 -17.647 0.000 -7.423 -5.940
age 0.082 0.006 14.344 0.000 0.071 0.094
totChol 0.002 0.001 1.940 0.052 0.000 0.004
currentSmoker1 0.443 0.094 4.733 0.000 0.260 0.627

Conditions for logistic regression

  1. Linearity: The log-odds have a linear relationship with the predictors.

  2. Independence: The observations are independent from one another.

Empirical logit

The empirical logit is the log of the observed odds:

\[ \text{logit}(\hat{p}) = \log\Big(\frac{\hat{p}}{1 - \hat{p}}\Big) = \log\Big(\frac{\# \text{Yes}}{\# \text{No}}\Big) \]

Calculating empirical logit (categorical predictor)

If the predictor is categorical, we can calculate the empirical logit for each level of the predictor.

heart_disease %>%
  count(currentSmoker, high_risk) %>%
  group_by(currentSmoker) %>%
  mutate(prop = n/sum(n)) %>%
  filter(high_risk == "1") %>%
  mutate(emp_logit = log(prop/(1-prop)))
# A tibble: 2 × 5
# Groups:   currentSmoker [2]
  currentSmoker high_risk     n  prop emp_logit
  <fct>         <fct>     <int> <dbl>     <dbl>
1 0             1           301 0.145     -1.77
2 1             1           318 0.158     -1.67

Calculating empirical logit (quantitative predictor)

  1. Divide the range of the predictor into intervals with approximately equal number of cases. (If you have enough observations, use 5 - 10 intervals.)

  2. Calculate the mean value of the predictor in each interval.

  3. Compute the empirical logit for each interval.

Then, create a plot of the empirical logit versus the mean value of the predictor in each interval.

Empirical logit plot in R (quantitative predictor)

emplogitplot1: for 1 quantitative variable

emplogitplot1(high_risk ~ age, 
              data = heart_disease, 
              ngroups = 10)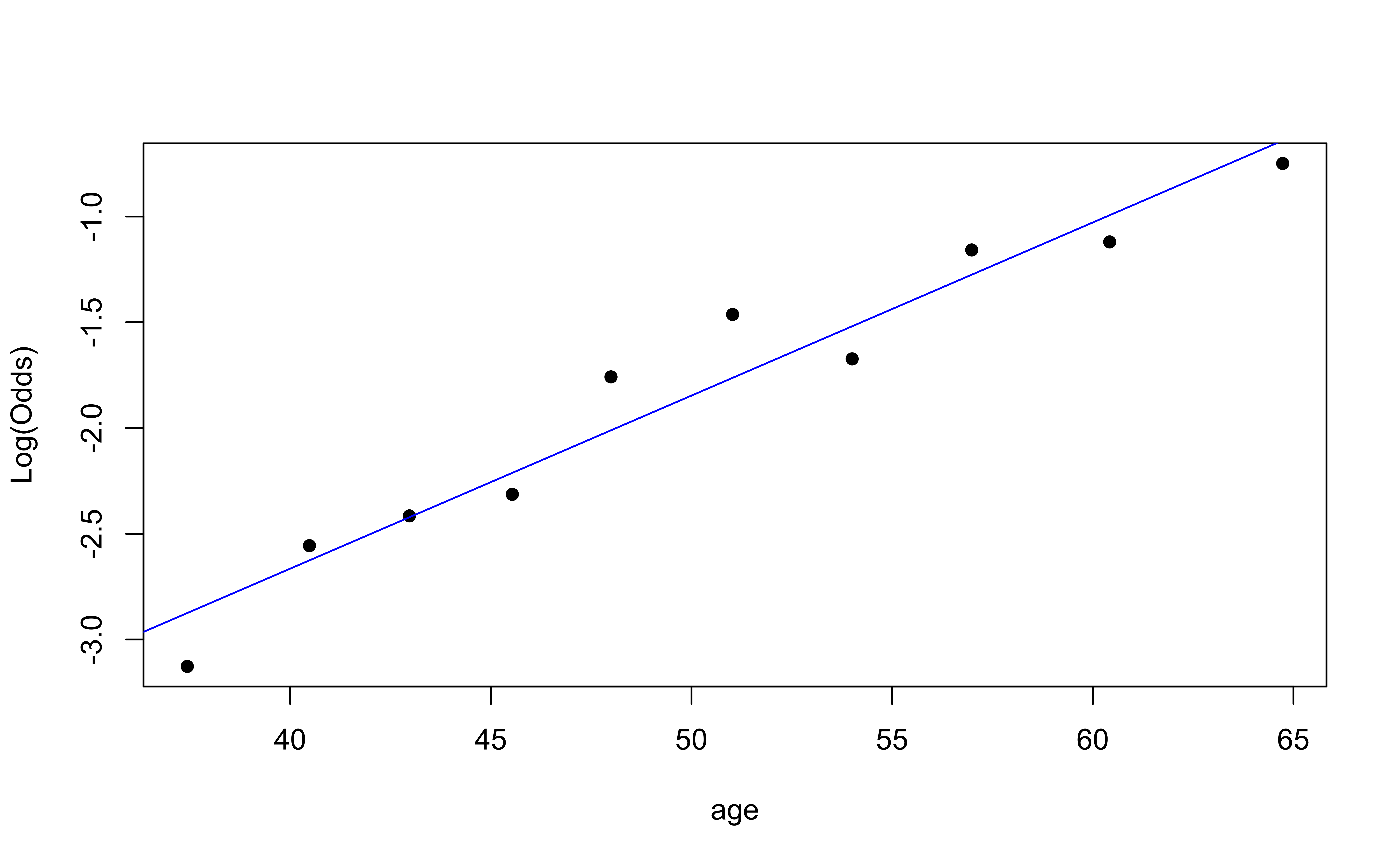

Empirical logit plot in R (interactions)

emplogitplot2: for 1 quantitative variable and 1 categorical variable

emplogitplot2(high_risk ~ age + currentSmoker, data = heart_disease, 
              ngroups = 10, 
              putlegend = "bottomright")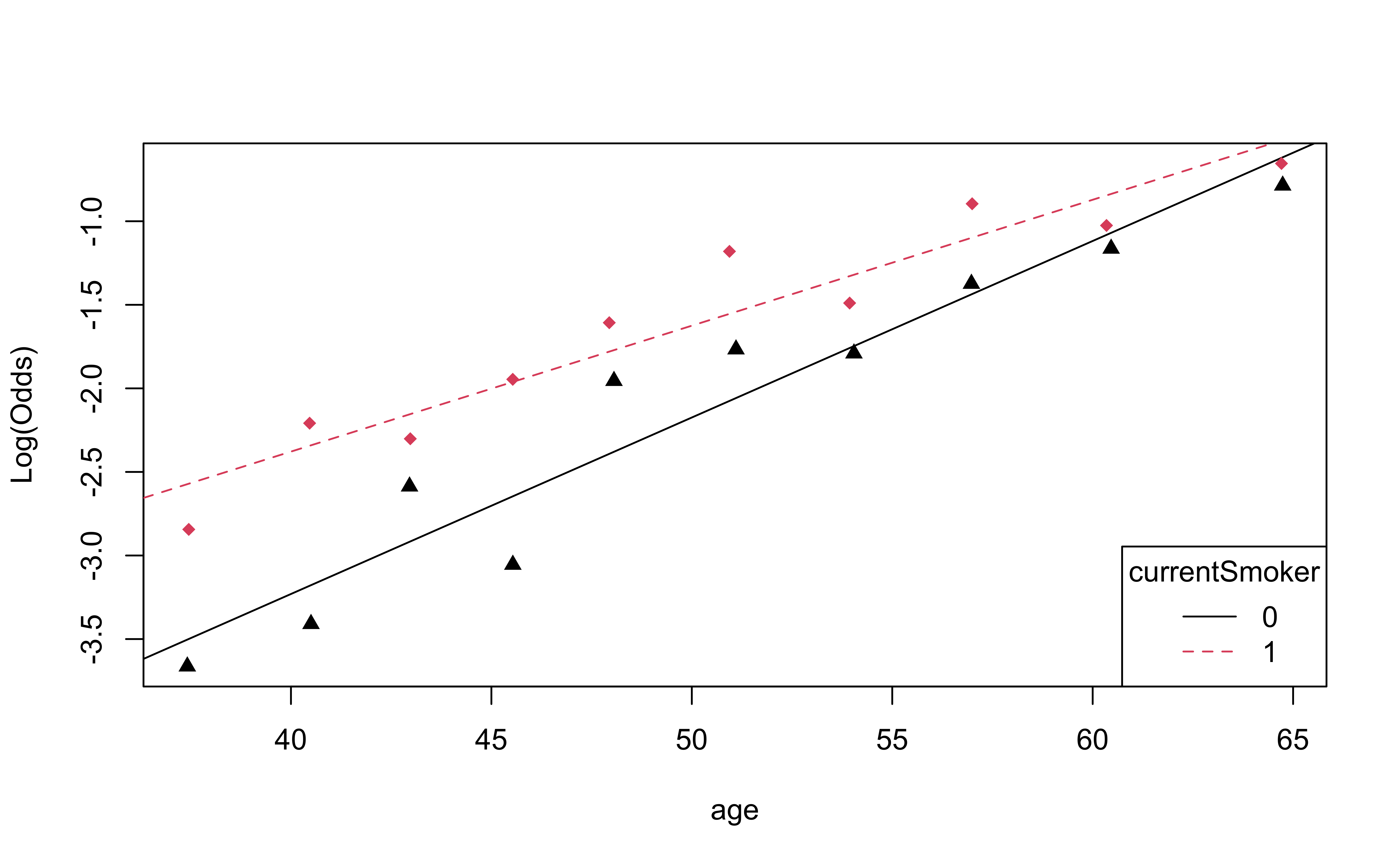

Checking linearity

emplogitplot1(high_risk ~ age, 
              data = heart_disease, 
              ngroups = 10)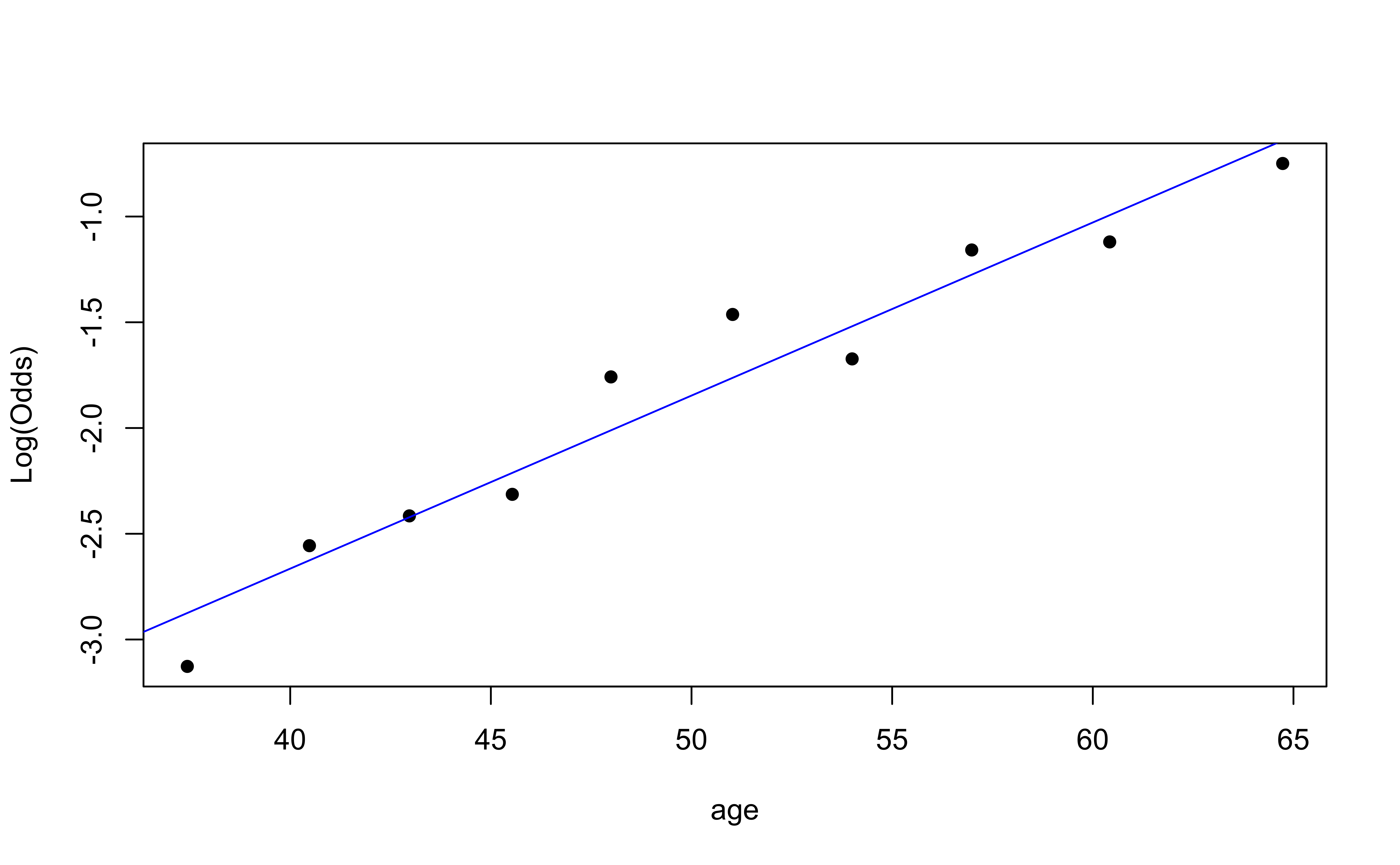

emplogitplot1(high_risk ~ totChol, 
              data = heart_disease, 
              ngroups = 10)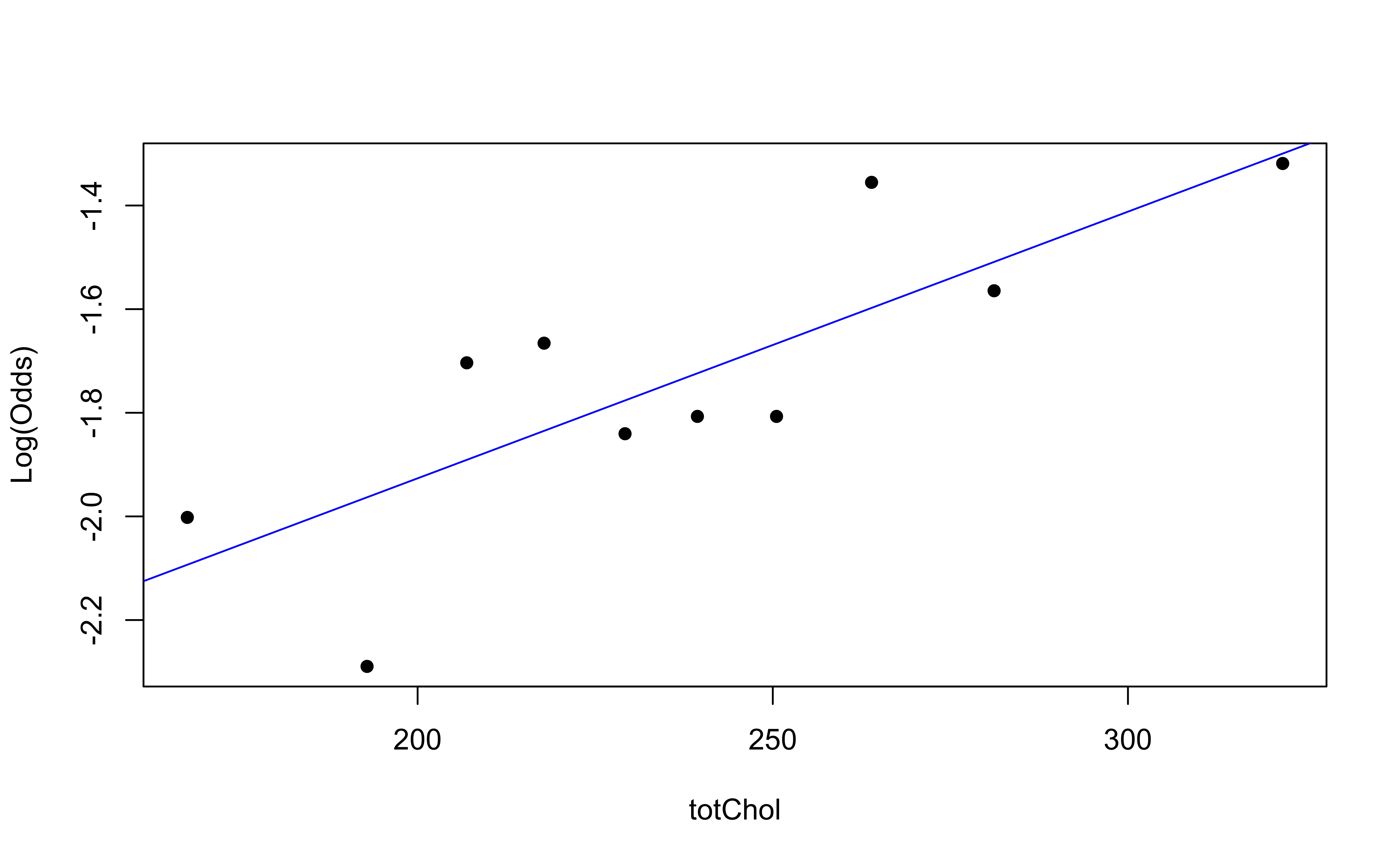

✅ The linearity condition is satisfied. There is a linear relationship between the empirical logit and the predictor variables.

Checking independence

  • We can check the independence condition based on the context of the data and how the observations were collected.
  • Independence is most often violated if the data were collected over time or there is a strong spatial relationship between the observations.

✅ The independence condition is satisfied. It is reasonable to conclude that the participants’ health characteristics are independent of one another.

Checking randomness

  • Randomness: The data were obtained from a random process

  • Was the sample randomly selected?

  • If the sample was not randomly selected, ask whether there is reason to believe the observations in the sample differ systematically from the population of interest.

  • We can check the randomness condition based on the context of the data and how the observations were collected. . . .

✅ The randomness condition is satisfied. We do not have reason to believe that the participants in this study differ systematically from adults in the U.S. in regards to health characteristics and risk of heart disease.

Comparison between logistic regression and linear regression

Linear Logistic
Outcome continuous binary
left side of equation y log odds
Inference CI + HT CI+HT
Comparison ANOVA(F-test), AIC, BIC, R-squared ANOVA(Drop-in-Deviance), AIC, BIC, AUC
Conditions linearity, independence, randomness, normality, constant variance linearity (log odds and predictors), independence, randomness

Application exercise for model comparison

📋 ae-10-flight-delays